Areal Distortions of Global Map Projections

This post may contain affiliate links. As an Amazon Associate, we earn from qualifying purchases.

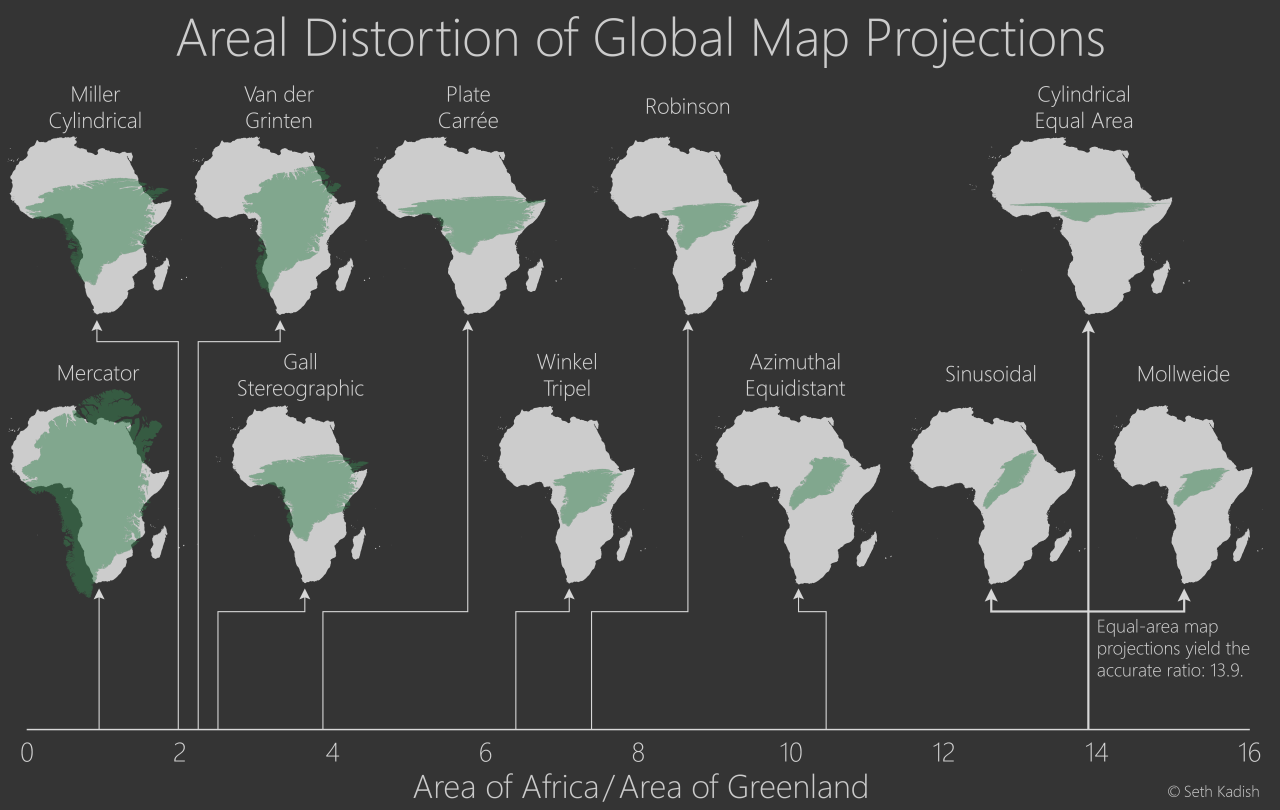
Mercator
A cylindrical map projection presented in 1569 by the Flemish geographer Gerardus Mercator. It became the standard map projection for nautical navigation because of its ability to represent lines of constant course, known as rhumb lines, as straight segments that conserve the angles with the meridians. Although the linear scale is equal in all directions around any point, thus preserving the angles and the shapes of small objects, the Mercator projection distorts the size of objects as the latitude increases from the Equator to the poles, where the scale becomes infinite.

Miller Cylindrical
A modified Mercator projection, proposed by Osborn Maitland Miller in 1942. The latitude is scaled by a factor of ​4⁄5, projected according to Mercator, and then the result is multiplied by ​5⁄4 to retain scale along the equator.

Gall Stereographic
A cylindrical projection, presented by James Gall in 1855. It is neither equal-area nor conformal but instead tries to balance the distortion inherent in any projection.

Van der Grinten
A compromise map projection, which means that it is neither equal-area nor conformal. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der Grinten projects the entire Earth into a circle. It largely preserves the familiar shapes of the Mercator projection while modestly reducing Mercator’s distortion. Polar regions are subject to extreme distortion.
This projection was presented in 1898 by Alphons J. van der Grinten.

Azimuthal Equidistant
The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth from the center point. A useful application for this type of projection is a polar projection which shows all meridians as straight, with distances from the pole represented correctly.

Robinson
The Robinson projection is a map projection of a world map which shows the entire world at once. It was specifically created in an attempt to find a good compromise to the problem of readily showing the whole globe as a flat image. The Robinson projection was proposed by Arthur H. Robinson in 1963.

Winkel Tripel
The Winkel tripel projection, a modified azimuthal map projection of the world, opposed by German cartographer Oswald Winkel in 1921. In 1998, the Winkel tripel projection replaced the Robinson projection as the standard projection for world maps made by the National Geographic Society.

Plate Carree
A simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100. The projection maps meridians to vertical straight lines of constant spacing, and circles of latitude to horizontal straight lines of constant spacing. The projection is neither equal-area nor conformal.

Cylindrical Equal Area
A projection in which meridians are mapped to equally spaced vertical lines and circles of latitude are mapped to horizontal lines. The only cylindrical projections that preserve area have a north-south compression precisely the reciprocal of east-west stretching (cos φ): equal-area cylindrical. This divides north-south distances by a factor equal to the secant of the latitude, preserving area but heavily distorting shapes.

Mollweide
The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for global maps of the world or night sky. The projection trades accuracy of angle and shapes for the accuracy of proportions in an area, and as such is used where that property is needed, such as maps depicting global distributions. The projection was first presented in 1805 by astronomer Karl Brandan Mollweide.

Sinusoidal
A Sinusoidal projection presented in 1570 by Jean Cossin of Dieppe. Scale is constant along the central meridian, and the east–west scale is constant throughout the map. Therefore, the length of each parallel on the map is proportional to the cosine of the latitude, as it is on the globe. This makes the left and right bounding meridians of the map into half of a sine wave, each mirroring the other. Each meridian is half of a sine wave with only the amplitude differing, giving the projection its name. Each is shown on the map as longer than the central meridian, whereas on the globe all are the same length.